2007年现代咨询方法与实务考核重点预测(第九章)
2007-02-15
普通
第九章 风险概率分析方法
大纲要求
1. 了解蒙特卡洛法;
2. 熟悉风险概率估算方法;
3. 掌握概率树分析法。
题型组合
1.变量概率的分布分析。计算变量概率的分析指标(期望值、方差、离散系数),确定变量的分布状态;
2.概率树的分析,画决策树,计算期望值,确定项目的风险程度;
3.利用蒙特卡洛模拟进行项目风险评价。
知识框架
1.风险概率估计

(2)风险变量概率的种类

(3)变量通常的概率分布
表9-1 变量的概率分布情况表
| 分布 | 内 容 | |
| 离散型概率分布 | 变量可能值是有限个数,概率取值之和等于1 | |
| 连续型 概率分布 |
正态分布 | 其特点是密度函数以均值为中心对称分布,其均值为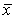 ,方差为 ,方差为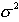 ,用N( ,用N(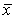 , , ) )表示。当 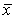 =0, =0, =1时,称为标准正态分布,用N(0,1)表示。适用于描述销售量、售价、产品成本等的概率分布 =1时,称为标准正态分布,用N(0,1)表示。适用于描述销售量、售价、产品成本等的概率分布 |
续表
| 分布 | 内容 | |
| 连 续 性 概 率 分 布 |
三角型分布 | 式中 n——离散变量的状态数 Xi——离散变量的第i种状态下变量的值 Pi——离散变量的第i种状态出现的概率 |
| β分布 | 方差的平方根成值为标准差,记为S | |
| 经验分布 | ||
(4)变量概率的分析指标
表9-2 变量概率的分析指标
| 指标 | 概念 | 计算 |
期望值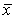 |
是变量的加权平均值 | 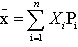 式中 n——离散变量的状态数 式中 n——离散变量的状态数Xi——离散变量的第i种状态下变量的值 Pi——离散变量的第i种状态出现的概率 |
| 方差 (S2) |
是描述变量偏离期望值大小的指标 |
方差的平方根称为标准差,记为S |
| 离散系数(β) | 是描述变量偏离期望值的离散程度的指标 | 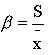 |
2.项目风险评价方法

(1) 概率树分析的步骤

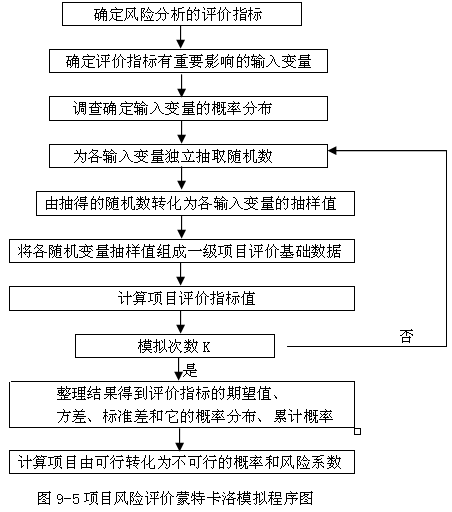
(2)蒙特卡洛模拟的程序
建设工程教育网原创·转载请注明出处