造价工程师答疑精华:年初年末等值

【提问】老师您好: 有个问题想请教。 某企业于第一年年初和第二年年初连续两年各向银行贷款30万,年利率为10%,约定于第三年、第四年、第五年三年年末等额偿还,则每年就偿还多少? [30*(1+10%)^6+30*(1+10%)^5]*10%/[(1+10%)^3-1]=30.65 某企业分两期向银行贷款,第一年年初贷款100万,第二年年初贷款200万,贷款利率6%,则相当于第一至三年内每年年末等额贷款约多少? [ 100*(1+6%)^4+200*(1+6%)^3]*6%/[(1+6%)^3-1]=114.5 两个题目的做法都一样,然而第二题的答案却是108万元。
【回答】学员您好:
第一题的解析:
第三年年初累计借款:P=30(1+10%)2+30(1+10%)=69.3(万元)
每年等额还款额:A= P[i(1+i)n]/[(1+i)n-1]=69.3[10%(1+10%)3]/[(1+10%)3-1]=27.87(万元)
第二题的解析:
三年末的贷款累计资金:F=100(1+6%)3+200(1+6%)2=119.1016+224.72=343.8216(万元)
每年年末需等额贷款A=Fi/[(1+i)n-1]=343.8216*6%/[(1+6%)3-1]=108(万元)
这两道题是有区别的,第一题属于现值计算求A,而第二题属于终值计算求A.
这部分内容在《工程造价管理基础理论与相关法规》P51.
不知道这样讲解您是否明白,如果还有不明白的我们再继续探讨。
【追问】我想问一下第一题,为什么第三年年未开始还款,而借款的终值只计算到第三年年初,第二年年未?
【回答】学员您好:
第三年年末开始还款时约定的。如题目所说。
您说的第二个问题:将借款换算到第三年年初,然后再换算成等额年金的形式,实际上是以第三年年初做了一个基准,而并不是说只计算到这里。关于复利计算的这几个公式里面都是包含了资金的时间价值的。
【追问】请老师画出上面第一题现金流量图,宾讲解一下
【回答】您好:
第一题的现金流量图为:

将头两年的现金流出这算到第2年作为P,在按照已知P求A的公式计算出3、4、5年的A第一题的解析:
第三年年初累计借款:P=30(1+10%)2+30(1+10%)=69.3(万元)
每年等额还款额:A= P[i(1+i)n]/[(1+i)n-1]=69.3[10%(1+10%)3]/[(1+10%)3-1]=27.87(万元)
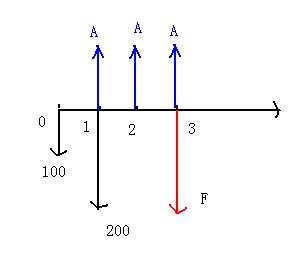
【追问】 每年年末需等额贷款A=Fi/[(1+i)n-1]=343.8216*6%/[(1+6%)3-1]=108(万元)
我觉得这里的n应该是2不是3 因为折到第三年末了,后面还剩第四和第五年了,怎么又多了一年呢?
【回答】学员yy7231,您好!您的问题答复如下:
做这样的题目,您可以画现金流量图来帮助理解:
根据以上现金流量图可以看出,已知终值求年金中的n为3年。
【追问】只有这么一种提法吗? 那,为什么说改革是社会主义发展的动力,是哪个答案呢?
【回答】您好,该问题的答案应该是教材73页面上从解放生产力,发展生产力来理解,把该段话的中心意思总结一下就是该题目的答案。请您按照我的思路练习一下。政治的论述题目虽然不同的人有不同的叙述,但只要抓住重点就都是对的。
责任编辑:天蓝